Skip to main content

Computing the horizon occlusion point

Kevin Ring

Are you sick of horizon culling yet? Great, me neither!

Last time, we explained what horizon culling is all about, and showed a very efficient way to test a point for occlusion by an ellipsoid. The objects we want to test for occlusion are rarely simple points, however. In particular, we’d like to be able to test terrain tiles for occlusion by the ellipsoid. But terrain tiles are complicated objects composed of thousands of vertices.

Deron Ohlarik addressed this in a previous blog post by explaining that, for any arbitrary geometry, we can compute the position of a point, which we call the horizon occlusion point, with a special relationship to the geometry. No matter what direction a viewer approaches the geometry from, the point will become visible to the viewer at the same time or before any part of the geometry becomes visible. This is exactly what we need! Many details of how to compute such a point were left as an exercise for the reader, however. Furthermore, it was unclear if this approach could be generalized to an ellipsoid rather than a sphere. This blog aims to fill in both of these gaps.

Once again, credit for the technique presented here is due entirely to Frank Stoner.

Let’s take a look at our situation. As before, we transform all of our coordinates to the ellipsoid-scaled space by multiplying each component, X, Y, and Z, by the inverse of the ellipsoid’s radii along that axis.

Math equations
Math equations
Math equations
Math equations
Math equations
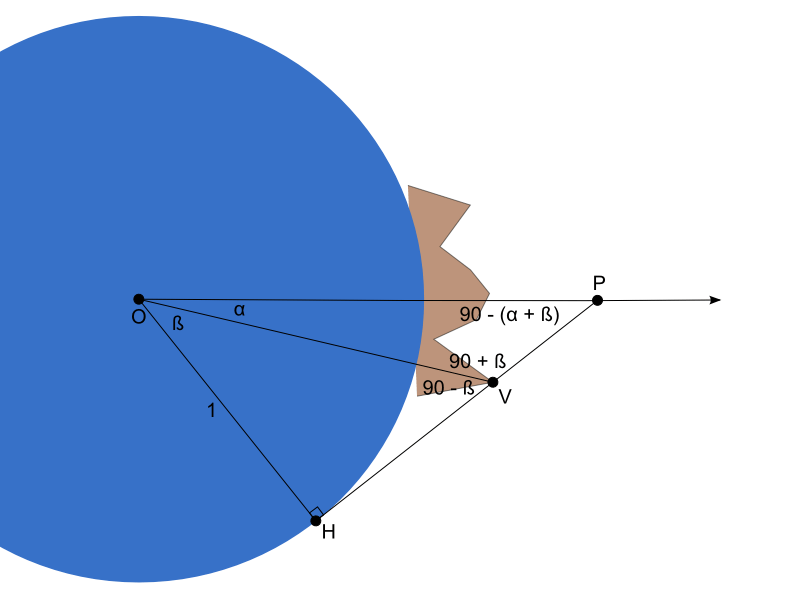
function computeMagnitude(ellipsoid, position, scaledSpaceDirectionToPoint) {
    var scaledSpacePosition = ellipsoid.transformPositionToScaledSpace(position);
    var magnitudeSquared = scaledSpacePosition.magnitudeSquared();
    var magnitude = Math.sqrt(magnitudeSquared);
    var direction = scaledSpacePosition.divideByScalar(magnitude);

    // For the purpose of this computation, points below the ellipsoid
    // are considered to be on it instead.
    magnitudeSquared = Math.max(1.0, magnitudeSquared);
    magnitude = Math.max(1.0, magnitude);

    var cosAlpha = direction.dot(scaledSpaceDirectionToPoint);
    var sinAlpha = direction.cross(scaledSpaceDirectionToPoint).magnitude();
    var cosBeta = 1.0 / magnitude;
    var sinBeta = Math.sqrt(magnitudeSquared - 1.0) * cosBeta;

    return 1.0 / (cosAlpha * cosBeta - sinAlpha * sinBeta);
}

As you can see, this computation is more expensive than the computation we described last time to test this point against the horizon. It’s probably possible to optimize it by testing each vertex using the cone test described previously and only computing the precise horizon occlusion point for the vertex if the vertex is found to be outside the cone. I’ll leave that as an exercise for the reader.

In any case, the cost of this computation is the main reason that it is primarily only appropriate for static geometry. If the geometry changes with respect to the ellipsoid, then this computation will need to be repeated on each change. That’s likely to get expensive.

Also, please keep in mind an important caveat when using this approach. In the real world, objects occluded by the WGS84 ellipsoid are not necessarily occluded by the real surface of the Earth. This is because the Earth’s surface is actually slightly below the ellipsoid in parts of the world. Depending on your application, using WGS84 as the occluding volume may be acceptable, or you may need to use a more conservative ellipsoid.