Horizon Culling
In developing virtual globes like Cesium, we need to be able to quickly determine when objects in the scene, like terrain tiles, satellites, buildings, vehicles, etc. are invisible and therefore do not need to be rendered. We do view-frustum culling, of course. But another important type of culling is horizon culling.
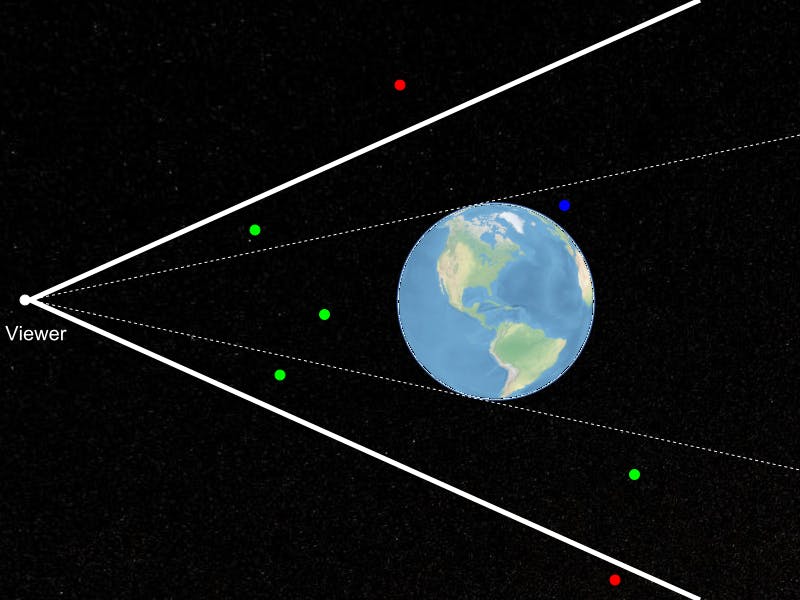
In the figure above, the green points are visible to the viewer. The red points are not visible because they are outside the view frustum, represented as heavy white lines. The blue point is inside the view frustum, but it is not visible to the viewer because it is occluded by the Earth. In other words, it is below the horizon. Horizon culling is the straightforward idea that you do not need to render objects that lie below the horizon as viewed from the current viewer position. As straightforward as this sounds, the details get tricky, especially because it needs to be very fast. Cesium will do this test hundreds of times per render frame in order to test the visibility of terrain tiles. It’s an important test, though. In the configuration in the figure above, terrain tiles covering the entire Earth lie inside the view frustum. Over half of them, however, are below the horizon and do not need to be rendered.
A few years back, Deron Ohlarik wrote two excellent articles on horizon culling. We’ve since developed an extension to his techniques that I would like to share here. While it only applies to static data like terrain tiles, we’ve found it to be very useful because it is both faster and more accurate than previous techniques. The accuracy improvement comes from horizon culling against an ellipsoidal model of the Earth rather than a spherical approximation.
I should mention up front that credit for this technique is entirely due to my colleague, Frank Stoner. My only contributions are implementing it in Cesium and writing about it here, after he did the hard work of deriving it.
Horizon culling a point against a sphere
As described by Ohlarik, for horizon-culling purposes, we can compute a bounding sphere for a static object like a terrain tile that is so tight that it is just a single point. If that point is below the horizon, then we can be sure that the entire tile is below the horizon, too. Our new technique is limited to culling a single point against an ellipsoid, so we start off assuming that this “occludee point” has already been computed. For details about how that is done, see the followup blog post.
I promised we would implement horizon culling against a general ellipsoid, and I’ll make good on that promise, but let’s start by using a simple unit sphere for horizon culling. Then, I’ll show that we can easily generalize this to an arbitrary ellipsoid. Consider the figure below:

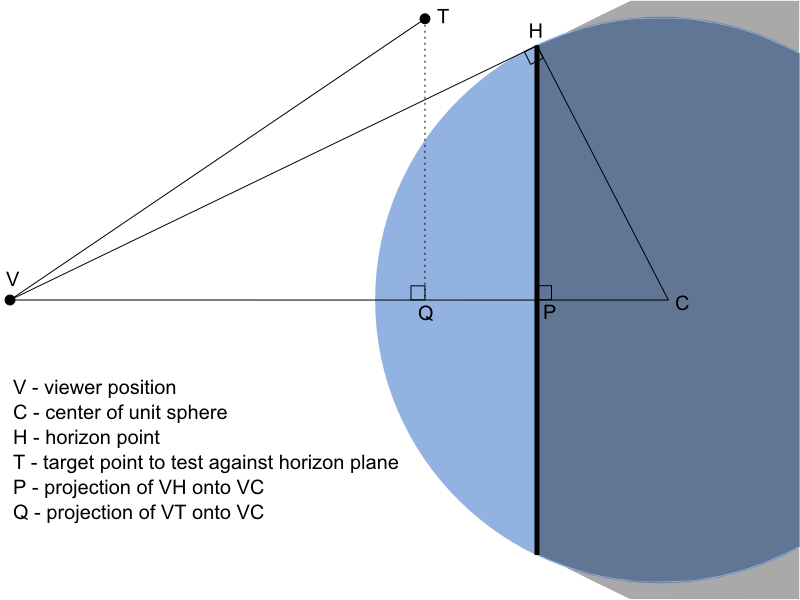
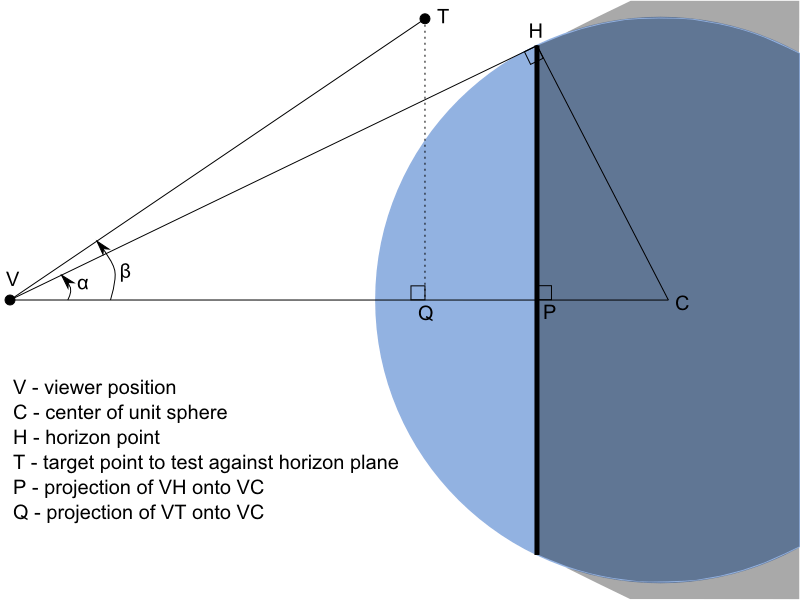
In this figure, the blue circle is our unit sphere. The lines extending from the camera position and tangent to the sphere represent the horizon. The black, vertical line represents all of the horizon points. On our unit sphere, the horizon points lie on a plane and form a circle. The vectors from the camera position to all horizon points form an infinite cone.
The portion of the sphere and the space around it that is shaded grey represents the region “below” the horizon. Any point in the shaded region is not visible from the camera position. Intuitively, the point is below the horizon if it is inside the infinite cone formed by the tangent vectors, and it is behind the plane containing all the horizon points.
The plane test
First, let’s develop an inexpensive test to determine which side of the plane a point is on. Consider the figure below:






// Ellipsoid radii - WGS84 shown here
var rX = 6378137.0;
var rY = 6378137.0;
var rZ = 6356752.3142451793;
// Vector CV
var cvX = cameraPosition.x / rX;
var cvY = cameraPosition.y / rY;
var cvZ = cameraPosition.z / rZ;
var vhMagnitudeSquared = cvX * cvX + cvY * cvY + cvZ * cvZ - 1.0;
Then, for each point we wish to test for occlusion culling:
// Target position, transformed to scaled space
var tX = position.x / rX;
var tY = position.y / rY;
var tZ = position.z / rZ;
// Vector VT
var vtX = tX - cvX;
var vtY = tY - cvY;
var vtZ = tZ - cvZ;
var vtMagnitudeSquared = vtX * vtX + vtY * vtY + vtZ * vtZ;
// VT dot VC is the inverse of VT dot CV
var vtDotVc = -(vtX * cvX + vtY * cvY + vtZ * cvZ);
var isOccluded = vtDotVc > vhMagnitudeSquared &&
vtDotVc * vtDotVc / vtMagnitudeSquared > vhMagnitudeSquared;
In Cesium, we pre-compute the scaled-space position instead of doing it before each test as shown above.
Future
Using this technique for terrain culling in Cesium allowed us to avoid drawing about 15% of the tiles we otherwise would have drawn in common scenes, versus our previous technique of culling with a minimum-radius bounding sphere. Happily, the new test is faster to execute for each tile as well!
One detail that we’ve skirted around so far is how we’re generating the “occludee” test points from our terrain tiles and other static geometry. Currently, we’re computing each tile’s occludee point based on the (false, but conservative) assumption that occlusion will be performed using a sphere formed from the minimum radius of the ellipsoid. By using a more accurate computation for the occludee point, we should be able to cull more tiles.
Update: This is covered in more detail in a followup post.
However, while the ellipsoid is a convenient and reasonably accurate surface for horizon culling, we must always keep in mind that real terrain is often below the ellipsoid. If we improve the computation of the occludee point, we must take care that the more accurate, relative to the ellipsoid, horizon culling does not end up culling tiles that are actually still visible, relative to the real terrain. This is especially likely to be a concern when rendering underwater terrain.